Aplicaciones
del ábaco de Smith
(12/2000)
(Publicación preliminar
Revisión 01/07/02)
Por Miguel R. Ghezzi (LU
6ETJ)
lu6etj @ solred.com.ar
SOLVEGJ
Comunicaciones
www.solred.com.ar/solvegj
(Para
visualizar los caracteres especiales precisa tener instalada en su
sistema la fuente Symbol)
Nota: El presente trabajo, en su primera fase, es
preliminar y está en proceso de revisión, por lo tanto puede contener
errores. También faltan completar temas tales como: la operación
con líneas con pérdidas y su aplicación práctica en redes de adaptación
de impedancias más complejas que empleen varios elementos de constantes
concentradas y/o líneas tipo "microstrip".
El radioaficionado que busca en
su actividad algo más que un pasatiempo y encara la afición en forma
creativa, al intentar obtener una mejor comprensión de los fenómenos que
involucra la radio, encuentra a menudo limitaciones teóricas que le
cierran el camino a su objetivo. Ciertos conocimientos que habitualmente
son propios de la ingeniería de radio se encuentran en libros
universitarios que presumen conocimientos teóricos previos, lo que
desalienta el intento y frustra sus iniciativas. El presente trabajo es
un intento para acercarle algunos elementos que le permitan encarar
algunos de los desafíos cotidianos
Existen herramientas muy
potentes que, si bien se enseñan en los últimos años de las carreras de
ingeniería, pueden comprenderse muy bien con los conocimientos propios
de un aficionado avanzado, aunque no profesional. Tal es el caso del
Abaco de Smith el cual abre las puertas a cuestiones que
parecen oscuras e insalvables. aunque precisa de algunas nociones
previas de mediana dificultad para el hobbista emprendedor. Este
artículo pretende explicar su uso con ejemplos, haciendo uso del mejor
esfuerzo de su autor para no sobreestimar la capacidad del lector. La
intención está centrada en soslayar la brecha que suele producir la
falta de una base universitaria en la teoría de los circuitos y las
matemáticas del campo complejo.
Lamentablemente no se puede
encarar una explicación útil de las posibilidades del ábaco sin
conceptos previos tales como: Resistencia, Reactancia, Impedancia,
Conductancia, Susceptancia, Admitancia, longitud de onda, velocidad de
propagación, relación de ondas estacionarias, coeficiente de reflexión,
fase, etc. Felizmente, estas cuestiones abundan en numerosos libros de
electrónica básica de radio y también en los radio handbooks.
El ábaco de Smith es un
formidable instrumento que de manera relativamente simple y con métodos
principalmente geométricos resuelve (y permite comprender mejor)
complicados procesos que se producen en las líneas de trasmisión y los
dispositivos adaptadores de impedancia los cuales, de otro modo,
requerirían herramientas matemáticas relativamente complicadas. Fue
creado por Phillip H. Smith de la RCA (1.905-1.987).
Son tantas y tan variadas las
posibilidades que brinda este nomógrafo, que solo tratar de mencionarlas
haría extender esta introducción mucho más allá de lo que ha ocupado,
por lo que apostaremos al lector paciente capaz de esperar hasta llegar
al final de camino para que paso a paso vaya descubriendo sus
posibilidades e infiriendo en cada uno todas las posibilidades que se
abren a cada paso.
Indice:
Descripción
geométrica del ábaco
Algunos
usos del ábaco
Descripción geométrica del ábaco
Previamente a la lectura de
todo el artículo tenga a mano un ábaco completo en papel con todas sus
inscripciones pues en la página web emplearemos una versión simplificada
para que la trasmisión de la información sea rápida. Haciendo clic aquí
Ud. podrá bajar una imagen detallada del ábaco con fines puramente
didácticos la cual no debería emplearse para el trabajo cotidiano pues
está protegida por los derechos de copyright de sus
propietarios.
Antes de comenzar dejaremos en
claro que el ábaco puede operar (y de hecho eso se hace constantemente)
con las inversas. En los ejemplos emplearemos Reactancia, Resistencia e Impedancia, pero debe
comprenderse que cualquier operación que pueda hacerse con estas
magnitudes podrá efectuarse con Susceptancia,
Conductancia y Admitancia. Todas
las líneas de referencia son duales: pueden representar la magnitud y su
inversa tal como está expresamente señalado en el mismo
ábaco.
El ábaco se presenta como un
círculo que en su periferia contiene varias escalas circulares
(dibujadas en esta página con celeste y amarillo) y en su interior tiene
dibujadas otras escalas. Es importante que observe cuidadosamente la
geometría del ábaco lo que también destacará lo ingenioso de esta
construcción.
Volver
al índice
Escalas de Resistencia y
Reactancia
La recta horizontal que pasa a
través del centro del ábaco se denomina "Eje de los
reales". Es una escala en la que se representará la parte
real de una impedancia compleja, es decir su
resistencia. Observe que ésta es la única línea recta
que posee.
El valor de resistencia
cero esta sobre la izquierda del eje y el valor de resistencia infinita sobre la derecha.
La
escala no es lineal y en su centro, que coincide con el centro del
ábaco, se representa la impedancia característica
de la línea de trasmisión que estemos analizando.
Habitualmente será 50 Ohms pero puede ser cualquier otro, 5 Ohms, 75
Ohms, 600 Ohms, etc. Muy frecuentemente este valor será 1 (uno)
sin que esto signifique que la línea de trasmisión tenga una Zo = 1,
sino que este valor será "la impedancia normalizada de la
línea" concepto que explicaremos muy pronto. Hay muchas
operaciones que podemos realizar con el ábaco y que no emplean líneas de
trasmisión, en este caso el centro será simplemente un punto de
referencia.
Círculos de Resistencia y Reactancia
constante
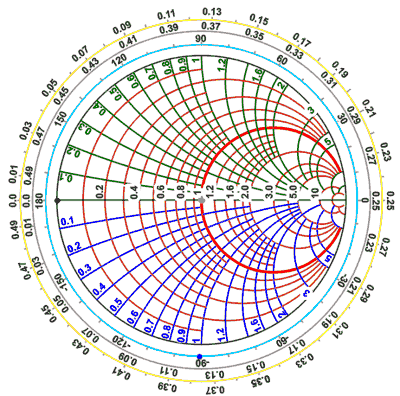Dentro del
ábaco encontraremos un grupo de varios círculos completos (aunque
por legibilidad no se dibujen completamente sobre el lado derecho),
cuyos centros están situados sobre el eje de los reales. Se denominan
"Círculos de resistencia
constante"; cortan al eje de los reales en dos
puntos: uno sobre el borde derecho correspondiente a resistencia
infinita y otro en distintos puntos del eje que identificarán con
su valor de resistencia al círculo correspondiente. Así
tendremos el círculo de resistencia constante de 10 Ohms, de 100 Ohms,
etc. Pronto veremos que quiere decir esto de "Resistencia Constante".
Estos circulos estan dibujados en color rojo en la figura de ejemplo.
También se dibujan
porciones de círculos cuyos centros están fuera del ábaco
y que se intersectan siempre en dos puntos con la circunferencia
exterior, uno de ellos sobre el valor infinito del eje de los reales y
el otro en el borde exterior calibrado en reactancia. Cada uno de estos
círculos representa un valor de reactancia y se denominan
"círculos de reactancia constante".
Los que están arriba del eje
de los reales corresponden a valores de reactancia
inductiva/susceptancia capacitiva (dibujados en color verde) y los que están debajo a reactancia capacitiva/susceptancia inductiva
(dibujados en color azul).
Estas porciones de circulo
intersectan la circunferencia exterior de forma perpendicular y así como
los círculos de resistencia constante eran todos tangentes al borde
derecho del ábaco, estos son tangentes al eje de los reales en R = ¥.
Observe que los círculos de
reactancia y resistencia constante también se intersectan entre si
perpendicularmente, por esta razón estas familias de círculos se
denominan "Familias de círculos ortogonales".
Volver
al índice
Las
escalas circulares exteriores
Pobre servicio nos prestaría el
ábaco si no contara con los círculos exteriores. Estos círculos nos
permitirán averiguar valores de impedancia y otros que dependen de la
posición sobre la línea de trasmisión porque, como ya sabemos, a
medida que nos desplazamos por una línea el valor de impedancia en cada
punto considerado será diferente (siempre y cuando la impedancia de
carga no coincida con el valor de Zo).
Las dos escalas exteriores están
calibradas en términos de longitudes de onda a lo largo de una línea de
trasmisión marcadas como: WAVELENGHT TOWARD GENERATOR (longitudes
de onda hacia el generador) y WAVELENGHT TOWARD LOAD (longitudes
de onda hacia la carga) (círculo amarillo de la figura).
La escala
del primero y más externo tiene su cero sobre el cero del eje de los
reales y se incrementa en sentido horario. El segundo lo hace en sentido
antihorario y su cero está donde la escala corta al eje de los reales en
R = ¥.
Note que son escalas iguales pero
opuestas.
Los valores de esta escala corresponden a posiciones
físicas en la línea medidas desde el generador o la carga en términos de
longitudes de onda: Suponiendo una longitud de onda de 1m, un punto de
la misma que esté situado 10 cm de la carga se encuentra a 0,1
l
"hacia el generador". Debe tenerse cuidado con esta escala, ella
es de lectura directa únicamente con valores puramente resistivos de
impedancia de carga (o generador). Luego veremos cómo se emplean.
Si observamos con cuidado,
veremos que en el punto en que la escala "WAVELENGHT TOWARD GENERATOR"
intersecta al eje de los reales en infinito se lee 0,25 l que corresponderá,
naturalmente, a un punto alejado 1/4 l de la carga. Ambas escalas
finalizan cuando alcanzan nuevamente el punto de partida en el valor 0,5
l y que
corresponde a un punto alejado 1/2 l de la carga o el generador
según la escala que estemos considerando.
Vemos entonces que la
circunferencia completa del ábaco representa 1/2 onda. Debe quedar claro
a partir de aquí que un grado sexagesimal en el ábaco corresponde a 0,5
grados eléctricos sobre la línea de trasmisión y por lo tanto 360°
sexagesimales corresponden a 180° eléctricos. Recordemos esto cuando
hagamos uso del transportador en el trabajo cotidiano.
Hay una tercer escala muy
importante denominada "ANGLE OF COEFICIENTE OF REFLECTION IN
DEGREES" (Angulo, o fase, del coeficiente de reflexión en grados, en
color celeste sobre la figura) cuyo cero está a la altura del valor
infinito del eje de los reales. Sobre el semicírculo superior se cuenta
en sentido antihorario desde 0° a 180° y sobre semicírculo inferior en
sentido horario desde 0° a -180°. Recordemos siempre que son "Grados
eléctricos".
Fuera del gráfico suelen
agregarse escalas rectas auxiliares denominadas "Nomógrafos radiales"
que ayudarán a obtener lecturas directas de algunos parámetros según se
verá luego.
Volver
al índice
Los
números normalizados
Puesto que las líneas de
trasmisión pueden tener cualquier valor de impedancia característica,
podría pensarse que es necesario un ábaco diferente para cada tipo de
línea, de hecho existen ábacos específícos para las líneas más usuales
tales como las de 50 Ohms pero lo usual es recurrir a un simple truco
para emplear siempre un mismo modelo independientemente de la Zo de la
línea que nos interesa. Para ello se recurre al procedimiento de
"normalización de unidades". El truco consiste en referir
todas las impedancias del problema al valor de impedancia característica
de la línea que estemos considerando.
En este tipo de ábaco (el más
común por cierto) el centro del gráfico corresponde al valor real 1
(uno) el que, a su vez, corresponderá al valor de la Zo de la línea
usada. Entonces:
-
Si la línea empleada es de 50
Ohms el valor "1" corresponderá a 50 Ohms. Si la línea empleada es de
75 Ohms el valor "1" corresponderá a 75 Ohms y así
sucesivamente.
-
Cualquier de impedancia puede
"normalizase" con el simple trámite de dividirla por la impedancia
característica de la línea considerada.
Ejemplos: Llamaremos
Z al valor que estamos normalizando y ZN al
normalizado. La Zo de la línea es de 50 Ohms.
Normalizar Z = 50 Ohms
(resistiva pura)
Z 50 Ohms 50
Ohms
Z = 50 Ohms =>
ZN = ---- = --------- = ---------- = 1
Zo
Zo 50 Ohms
Normalizar Z = 100 + j100
Ohms (inductiva)
Z = 100 + j100 => ZN = Z/Zo =
100/Zo + j(100/Zo) = 200/50 + j200/50) = 2 +
j2.
Normalizar Z = 25 - j50 Ohms
(capacitiva)
Z = 25 - j50 => ZN = Z/Zo =
(25 - j50)/50 = 25/50 - j(50/50) = 0,5 -
j1
Para desnormalizar los valores
obtenidos con nuestros trabajos sobre el gráfico y obtener los valores
verdaderos basta con el procedimiento inverso: Z = Zo x
ZN, es decir que multiplicamos por Zo al valor
normalizado Zn obtenido mediante alguna operación el ábaco.
Por ej. Al realizar cierta
operación sobre el ábaco obtenemos un punto en el gráfico ZN
= 1,5 + j1,5, ¿qué valor de impedancia representa si la línea es de 50
Ohms?
Z = Zo x ZN = 50 (1,5 + j1,5) =
50 x 1,5 + j0 x 1,5 = 75 +
j75
Volver
al índice
Algunos usos del ábaco
Representando impedancias en el
ábaco
Para representar un valor
cualquiera de impedancia, basta buscar la intersección del
círculo de resistencia constante que corresponde al valor resistivo de
la impedancia, con el círculo de reactancia constante correspondiente al
valor reactivo de la misma (advierta que la superficie del ábaco es el
lugar geométrico de todos los valores posibles de impedancia que pueden
existir).
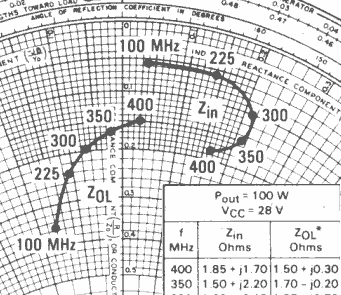
Una de las aplicaciones comunes
de esta manera de graficar consiste en la representación de valores de
impedancia que varíen conforme a algún parámetro de los que un sistema
sea dependiente tal como la frecuencia, potencia, temperatura, etc. Es
una forma frecuente de representar características de transistores de
radiofrecuencia en los manuales, como se ve en la figura.
Ejemplo: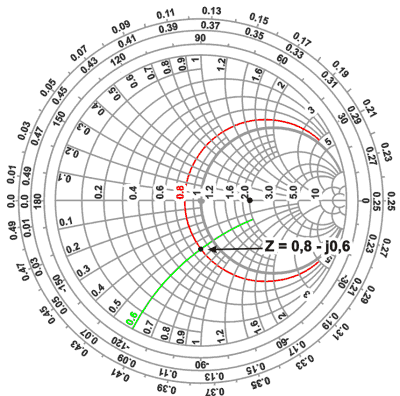
Conectamos al extremo de una
línea de Zo = 50 Ohms una carga ZL = 40 - j30 Ohms
y deseamos representar su valor en el ábaco.
La normalizamos para trabajar
sobre un ábaco estándar:
ZN = Z/Zo =
(40 - j30) W / 50 = 0,8 - j0,6
Para dibujar este punto en el
ábaco se busca el valor 0,8 sobre el eje de los reales
(correspondiente a valores resistivos) por este punto pasará un círculo
de resistencia constante correspondiente a este valor que señalaremos de
un modo conveniente.
Inmediatamente buscamos el valor
0,6 sobre borde del gráfico en la escala de reactancias
capacitivas (-j denota reactancia capacitiva y +j inductiva) y al
que también señalaremos de algún modo.
La impedancia 0,8 - j0,6 quedará
representada en el punto de intersección de los dos círculos que
hemos señalado.
Volver
al índice
El círculo de Gamma
constante
Ahora tracemos un círculo con
centro en el centro del ábaco y que pase por el punto que representa la
impedancia. El círculo que hemos
dibujado se denomina "Círculo de Gamma constante", Con él
se puede averiguar el valor del coeficiente de reflexión, para ello se
mide el radio de este círculo y se lo divide por el radio del ábaco, En
nestro caso el resultado debería ser aproximadamente 0,33 (recordemos
que el coeficiente de reflexión se puede definir como: r = Ö Pr/Pi. donde Pr =
Potencia reflejada y Pi = potencia incidente).
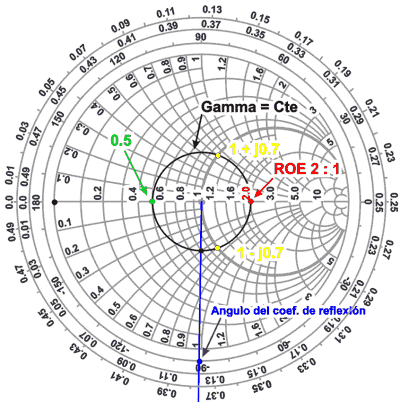Vemos que este
círculo corta al eje de los reales en dos puntos: En el que está a la
derecha del centro (en
rojo) se
puede leer directamente la Relación de Ondas Estacionarias, que
en este ejemplo será igual a 2 : 1.
Si se midiera la tensión en este
punto sobre la línea de transmisión, se vería que la tensión es máxima
(la corriente medida sería la mínima).
Igualmente, en el punto de
intersección del círculo de Gamma constante distante 1/4 de onda, sobre
el eje leeremos la inversa del valor de la ROE (0,5 en verde) y, si se midiera la tensión
sobre la línea en este punto resultaría ser un mínimo (la corriente un
máximo).
Dibujemos ahora una semirrecta
que parta del centro del gráfico, que pase por el punto que representa
la impedancia del ejemplo anterior y se prolongue hasta el borde del
ábaco, el punto de intersección de la recta trazada desde centro al
borde sobre la escala marcada "ángulo del
coeficiente de reflexión" representa la fase del
coeficiente de reflexión (el ángulo con que la onda reflejada atrasa o
adelanta respecto de la incidente) que en nuestro ejemplo será de
-90° y que está indicado en azul.
Cuando estas ondas se suman en
fase dan un máximo de tensión, la impedancia es puramente resistiva y
mayor que cero y el ángulo del coeficiente de reflexión es
cero.
De aquí en adelante iremos
viendo distintos ejemplos explicados con más detalle para comprender el
funcionamiento del ábaco.
Volver
al índice
La
línea como transformador de impedancia
Nuestro ejemplo nos ha dado una
información quizás más importante que la que buscamos
originalmente:
Los puntos situados sobre el
círculo de de Gamma constante representan todas las
impedancias posibles de encontrar a lo largo de la línea de trasmisión
para esa carga. Esto también nos advierte que todas esas
impedancias se corresponden con uno y solo un valor de ROE, lo
cual es otra muestra de que la ROE no varía a lo largo de una
línea de trasmisión (y que de nada sirve buscar, a estos
efectos, algún punto "privilegiado" recortando el cable, aunque
también es cierto que en una línea con pérdidas la ROE va disminuyendo
lentamente a medida que nos alejamos de la carga debido a
ellas)
Pero reflexione en lo
siguiente: Si la impedancia en la línea a 10 cm de la carga tiene un
dado valor, podemos imaginar que si la cortáramos en ese punto e
instaláramos allí una carga con una impedancia igual al valor leido en
el ábaco para ese punto, el resto de la línea no se enteraría del
"fraude", de esto podemos deducir otro dato fundamental: los
valores que atraviesa el círculo de gamma constante son todos
los valores (y los únicos), de impedancia posibles capaces
producir una ROE de 2 : 1 en una línea de 50
Ohms...
Observe que ningún punto del
círculo de Gamma constante pasa por R = 1 (el centro del ábaco
que correspondería, desnormalizando, a 50 Ohms). Esto nos muestra que no
existe ningún punto a lo largo de la línea que presente 50 Ohms
puramente resistivos (lo que también echa por tierra cualquier
fantasía acerca de adaptar la impedancia recortando el cable) pero
¡el c;irculo de Gamma constante si
corta al círculo de resistencia constante = 1, por lo que si es posible obtener 50 +/- jX siempre!,
lo cual ya nos está insinuando una manera correcta de adaptar una
impedancia de carga cualquiera a un
generador cuya ZG sea de 50 Ohms, como veremos en otro
ejemplo. En el actual esto se produce en los puntos Z = 1
± j0,7 (indicados en amarillo) que equivalen
(desnormalizando) a una impedancia de 50 ± j35, por lo tanto, si
logramos cancelar los 35 Ohms capacitivos o inductivos con un elemento
con una reactancia igual pero de signo opuesto ¡ya habremos logrado la adaptación...!
Puesto que la ROET es la misma,
es el mismo también el coeficiente de reflexión por lo tanto la relación
entre la potencia incidente y la reflejada en todos los puntos de una
línea sin pérdidas.
Volver
al índice
Convirtiendo Impedancias en
Admitancias y viceversa
Es muy fácil convertir
Impedancias en Admitancias y viceversa con el ábaco. Una vez graficado
el punto correspondiente a la Impedancia, basta trazar una línea que,
partiendo desde él y pasando por el centro, intersecte al círculo de
Gamma constante sobre el lado opuesto. En dicha intersección podremos
leer directamente el valor de Conductancia y Susceptancia.
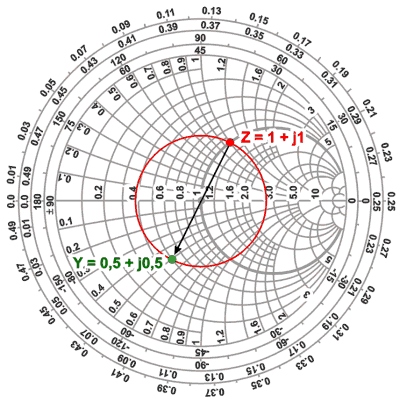Ejemplo:
Tenemos una impedancia Z = 50 +
j50 W
¿cuál es su Admitancia?
Normalizamos ZN = (50
+ j50) / 50 = 1 + j1 y lo marcamos en el gráfico.
Trazamos el círculo de Gamma
constante que pasa por él y dibujamos la línea que pasando por el centro
intersecte al círculo de Gamma constante sobre el lado opuesto, allí
leemos directamente:
Y = 0,5 -j0,5 [Mhos]
Teniendo la Admitancia, podemos
expresar nuestra impedancia en su equivalente paralelo de la forma Zp =
Rp ± Xp, para ello basta con obtener las
inversas de G y B, entonces:
Rp = 1 / G = 1 / 0,5 = 2
W ; Xp
= 1 / B = 1 / 0,5 = 2 W, que desnormalizado corresponderá a Rp = 100
W; Xp =
100 W.
Esto nos será muy útil como
veremos en los párrafos siguientes para adaptar impedancias en la
práctica y construir Stubs.
Volver
al índice
Cálculo de la impedancia vista por
el generador
Ejemplo:
Una línea con Zo = 50 Ohms, 6 m de longitud
y velocidad de fase = 0,66 se conecta a una carga ZL = 50 +
j50 W.
¿Cuál es la impedancia vista en los bornes correspondientes del
generador en 14,1 MHz?. (Ver la figura que se encuentra más
abajo).
1) Se normaliza la impedancia de
carga
50W
+ j50W
---------- = 1 +
j1
50W
2) Se calcula la longitud de onda en el
vacío correspondiente a 14,1 MHz
l = 3 x 108 [m/s] / 14,1 x 106
[Hz] = 21,3 [m]
3) Se determina la longitud de onda en el
coaxil (cuya velocidad de fase de 0,66).
lc = 0,66 x 21,27 m = 14,03 m (que naturalmente
corresponderán a una longitud eléctrica de 360°).
4) Se averigua la cantidad de longitudes de
onda en coaxil que representan los 6 m de línea:
ll = 6 m / 14,03 m = 0,428 de landa
4 bis) Se calcula la longitud
eléctrica correspondiente a los 6 m de la línea.
q = 360° * 6m / 14 m = 154,28 grados eléctricos que en grados
sexagesimales del gráfico serán 308,56°.
5) Se representa en el gráfico la
impedancia Z = (1+ j1).
6) Se traza el círculo de Gamma
constante que pasa por el punto Z (nos indicará una ROET = 2,6 :
1)
7) Se traza una semirrecta desde el centro
hasta la escala WAVELENGHT TOWARD GENERATOR que pase por el punto
Z (cae aprox. en el valor 0,161 landas hacia el
generador).
8) A partir de este valor se suma el valor
de longitud de la línea expresada en longitudes de onda calculado
(0,428), entonces 0,161 + 0,428 = 0,589, pero 0,589 no es un valor que
esté indicado en la escala que solo alcanza hasta 0,5, entonces
simplemente se resta 0,5 y obteniendo 0,089
9) Se dibujar otra semirrecta desde el
centro hasta la escala en el punto 0,089.
10) La intersección de esta semirrecta con
el círculo de Gamma constante da la impedancia buscada.
Z = 0,5 + j0,5 que desnormalizada
(multiplicando por Zo) es Z = 25 + j25 W
El proceso realizado se denomina
rotación pues en el ábaco se realiza una rotación geométrica con
centro en el mismo.
Es muy interesante advertir que es posible
proceder a la inversa, es decir, que conociendo la impedancia en los
bornes de entrada de nuestra línea de trasmisión, podremos averiguar la
impedancia de la antena, dicho de otro modo: si la impedancia medida
sobre el lado del generador fuera Z = 125 - j27 (que es el resultado
anterior), obviamente la impedancia de carga sería ZL = 50 -
j50 W
que justamente fue el dato de nuestro problema.
Nótese que si se realiza una rotación de
0,5 l
que corresponde a 360° en el gráfico se llega
exactamente al mismo punto del gráfico lo que significa que cada 1/2 se
repite la impedancia. Este fenómeno es muy útil pues si se corta
la línea de alimentación de una antena en múltiplos de media onda (en
coaxil) podemos efectuar mediciones directas en el lado del generador
sin tener que transformarlas para averiguar el verdadero valor, (siempre
con la reserva de que en FME normalmente una longitud de línea
normal representa muchos "largos de onda" y el error en la velocidad de
fase supuesta del coaxil puede producir mediciones absolutamente erradas
por la acumulación de errores).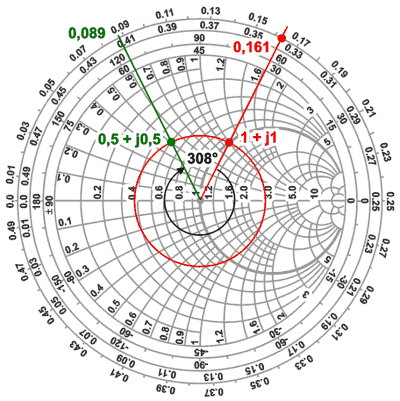
Si este procedimiento le resulta confuso en
términos de longitudes de onda, es posible proceder empleando grados
eléctricos y sexagesimales para la construcción gráfica:
1) Se normaliza la impedancia de
carga
50 - j50
--------- = 1 -
j1
50
2) Se calcula la longitud de onda
correspondiente a 14,1 MHz
l = 3 x 108 [m/s] / 14,1 x 106
[Hz] = 21,3 m
3) Se determina la longitud de onda en el
coaxil (velocidad de fase de 0,66).
lc = 0,66 x 21,27 m = 14,03 m (que naturalmente
corresponderán a una longitud eléctrica de 360°).
4) Se calcula la longitud eléctrica
correspondiente a los 6 m de línea.
q = 360° * 6 m /
14 m = 154 grados eléctricos que en grados sexagesimales del gráfico
serán 308°.
5) Representamos en el gráfico nuestra
impedancia Z = (1+ j1).
6) Se traza el círculo de Gamma constante
que pasa por el punto Z (indicará una ROET = 2,6 :
1).
7) Colocar un transportador con su centro
en el centro del gráfico y su 0 en el punto Z, medir 308°
(correspondiente a los los 154 grados eléctricos de la
línea) y marcar ese punto en el círculo de Gamma constante, allí
se encuentra el valor de impedancia que ve el generador: Z = 0,5 +
j0,5 que desnormalizada (multiplicando por Zo) es Z = 25 + j25
W.
Volver
al índice
Inductores y capacitores realizados
con secciones de línea
Las líneas de trasmisión que tienen el
extremo correspondiente a la carga en cortocircuito o abierto, tienen
interesantes propiedades, entre ellas la de permitir la obtención de
reactancias tanto inductivas como capacitivas. En general:
- Toda sección de línea de longitud
menor que 1/4 l cortocircuitada
en un extremo, presenta reactancia puramente inductiva en el
otro.
- Toda sección de línea de longitud
menor que 1/4 l en
circuito abierto en un extremo, presenta reactancia
puramente capacitiva en el otro.
- Toda sección de línea menor que 1/2
l, pero mayor que 1/4 l cortocircuitada en un extremo, presenta reactancia puramente
capacitiva en el otro.
- Toda sección de línea menor que 1/2
l pero mayor que 1/4 l en circuito
abierto en un extremo, presenta
reactancia puramente inductiva en el otro.
Normalmente en FME o FUE la calidad de los
inductores obtenidos con este método es superior a elementos de
constantes concentradas (bobinas solenoide comunes).
En el ábaco un
cortocircuito queda representado en el punto 0 (cero) del eje de los
reales, si nos dirigimos hacia el generador las longitudes de línea que
caen sobre todo el semicírculo inferior nos darán reactancias
capacitivas, esto corresponde a longitudes eléctricas menores que 1/4
l. Si seguimos recorriendo, superando el cuarto de onda nos
encontramos, en el semicírculo superior, y la línea nos presentará
reactancias inductivas.
Dejando la línea a circuito abierto, vemos
que un circuito abierto se representa sobre el extremo derecho del eje
de los reales que corresponde al valor de resistencia
infinito; igual que antes, dirigiéndose
hacia el generador a partir del circuito abierto, todas las longitudes
de línea que se representan sobre el semicírculo inferior corresponden a
reactancias capacitivas y longitudes menores que 1/4
l y todo el semicírculo superior corresponde a reactancias
inductivas y longitudes mayores que 1/4 l pero menores
que 1/2 l. Debe tenerse en cuenta que la escala calibrada en
longitudes de onda tiene indicado el valor 0,25 donde coincide con el
eje real en infinito, de manera que no hay que olvidarlo en el momento
de usarla.
Ejemplo: Se necesita en 144 MHz, un inductor de de 0.11 uHy ¿con
qué longitudes de una línea de Zo = 50 W, velocidad de fase
= 0,66, lo puedo obtener y en qué condiciones?.
1) Se calcula la reactancia correspondiente
a 0,11 uHy pF en 144 MHz
XL = 2 x p x f x L = 2 x 3,14 x 144 x
106 [Hz] x 0,11 x 10-6 [Hy] = 100
W
2) Se normaliza el valor de XL
dividiéndolo por la Zo de la línea
XLN = 100W /
50W = 2
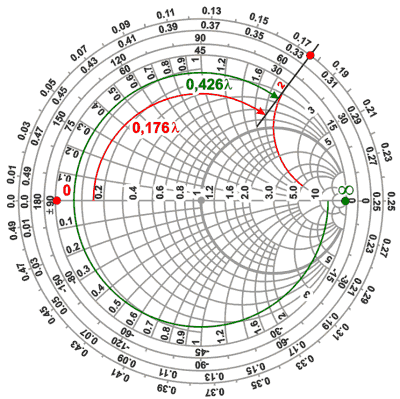3) Partiendo de una
sección de línea con el extremo en cortocircuito, recorriendo la
escala calibrada en longitudes de onda hacia el generador
(sentido horario), partiendo del valor en el eje real que corresponde a
0 Ohms, buscamos el circulo de reactancia constante XL = 2
(que corresponde al semicírculo superior). Observamos que corresponde a
una longitud de línea de 0,176 l.
3 bis) Partiendo de una sección
de línea con el extremo abierto, recorriendo la escala calibrada
en longitudes de onda hacia el generador (sentido horario)
partiendo del valor en el eje de los reales que corresponde a
resistencia infinita, buscamos el círculo de reactancia constante XL = 2
(que corresponde al semicírculo superior). Observamos que corresponde a
una marcación 0,176, pero en este caso habrá que agregar los
0,25l que
recorrimos desde el valor infinito hasta el cero para alcanzar el valor
buscado, por lo tanto el resultado será 0,25l + 0,176l= 0,426l
4) Calculamos la longitud física
de una longitud de onda en el coaxil:
lc = (3 x 108 [m/s] /
144 x 106 Hz) x 0,66 = (300 / 144) x 0,66 = 1,375 m
5) Multiplicamos los
valores obtenidos en el punto 3 y 3 bis por la longitud de onda física
que acabamos de calcular obteniendo:
Longitud de línea en
cortocircuito: 0,176 x 1,375 m = 0,242 m
Longitud de línea a circuito
abierto = 0,426 x 1,375 m = 0,585 m
Nota: En general conviene
emplear secciones a circuito abierto pues es más sencillo ajustarlas
cortándolas y porque es mucho más sencillo lograr un buen circuito
abierto que un buen cortocircuito en FME y FUE.
Volver
al índice
Adaptación de impedancias
mediante secciones de línea
Según se dijo en la sección correspondiente
al cálculo de la ROET, dada una carga cualquiera siempre será
posible encontrar algún punto en la línea que presente una parte
resistiva igual a Zo con alguna componente reactiva asociada (ello se
desprende de ver que el círculo de Gamma constante siempre
intersecta al círculo de resistencia normalizada unitario, que
desnormalizada correspondería a R = Zo). Si canceláramos la parte
reactiva en ese punto y lo conectáramos al generador, tendríamos una
adaptación perfecta... Pero nada impide conectar en ese punto otra línea
de trasmisión de la misma impedancia y de largo arbitrario que llegue
hasta el generador, algo así como un "prolongador", visto de ese modo,
el punto de la línea que presenta una resistencia igual a Zo pero con la
componente reactiva que cancelamos de alguna manera, se convierte en la
"carga" para la línea prolongadora y ella verá una carga perfectamente
adaptada por lo que no presentará ondas estacionarias ni producirá
ninguna variación de impedancia posterior.
En la práctica, una vez localizado el punto
apropiado sobre la línea, se procede a intercalar allí el componente
encargado de cancelar la reactancia y continuar la misma línea hasta el
generador.
En general el procedimiento es como
sigue:
- Normalizar la impedancia de carga y
graficarla en el ábaco.
- Trazar una línea del centro que pase por
ese punto y que intersecte la escala WAVELENGHT TOWARD GENERATOR
anotando a continuación el valor en longitudes de onda que indique la
escala (lo llamaremos lL).
- Dibujar el círculo de Gamma
constante.
- Marcar sobre el círculo de Gamma
constante los puntos (dos) donde intersecta al círculo de componente
resistiva unitaria, los llamaremos P1 y
P2, respectivamente .
- Trazar sendas líneas que, pasando por
P1 y P2 intersecten la escala WAVELENGHT TOWARD
GENERATOR. Leer en ella el valor de longitud de onda correspondiente a
P1 y P2 que llamaremos l1 y
l2.
- Averiguamos la distancia sobre las
escala de longitudes de onda que separa l1 de
lL y
l2 de
lL, a
estos resultados los llamamos L1 y
L2, representando cada uno de ellos la distancia de
la carga a la que se encuentran puntos de impedancia con componente
resistiva igual a Zo, (expresada en longitudes de onda). En cualquiera
de esos puntos podremos intercalar un elemento en serie que cancele la
reactancia existente en ellos para obtener la adaptación
deseada.
- Encontrar para
P1 y P2 el círculo de reactancia
constante que pasa por él (será uno de reactancia inductiva y el otro
de reactancia capacitiva). Estos valores de reactancia son los que
intercalados en los lugares hallados en el punto anterior permiten
adaptar la impedancia a la línea. Pero atención, la reactancia debe
ser de caracter opuesto a la leída.
- Elegir P1 o P2
de acuerdo a la conveniencia física del problema (a veces el
primer punto está muy cerca de la carga y resulta incómodo para
intercalar el componente reactivo).
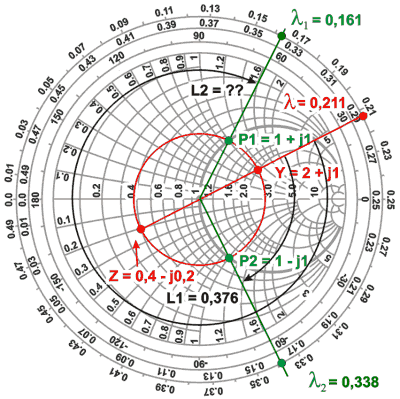
Ejemplo:
Tenemos una impedancia de 20 - j10
(capacitiva) alimentada por una línea de 50 ¿A qué distancia de la
carga, qué tipo de elemento y de qué valor hay que intercalar para que a
partir de ese punto la línea quede adaptada?
Normalizamos la impedancia de
carga
ZN = ZL / Zo = (20 -
j10) / 50 = 0,4 - j0,2
Trazamos la semirrecta que pasa por
ZL y obtenemos lL = 0,462
Trazamos las semirrectas que pasan por
P1 y P2
y obtenemos:
l1 = 0,161 ;
l2 = 0,338
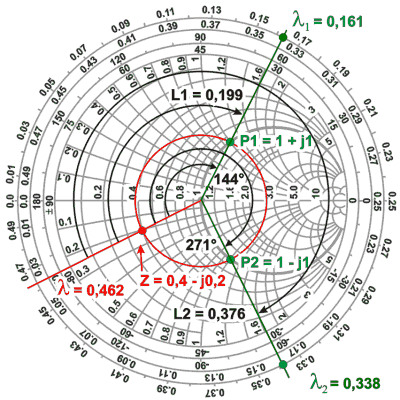Aquí hay que tener cuidado pues en todos los casos hemos
indicado las lecturas sobre la escala WAVELENGHT TOWARD GENERATOR que
aumenta en sentido antihorario, pero no debemos simplemente restarlas
sino determinar la distancia que las separa sobre la escala. Esto es
sencillo:
Si observa el gráfico v que que resulta de ver qué
distancia le falta a lL para alcanzar 0,5 (que coincide
con el cero de la escala), es decir 0,5 - lL y a ese
valor se le suma la lectura de l1 y l2,
podemos evitar esta cuenta con solo leer la lectura que muestra
lL sobre la escala WAVELENGHT TOWARD LOAD
(verifíquelo). Entonces:
0,5 - lL = 0, 5 - 0,462 =
0,038
L1 = l1 + 0,038 = 0,161 +
0,038 = 0,199
L2 = l2 + 0,038
= 0,338 + 0,038 = 0,376
A estas distancias de la carga
encontraremos los puntos en los cuales intercalando una reactancia
en serie del valor adecuado lograremos la transformación
que resulte en los 50 Ohms deseados. Leyendo en el gráfico vemos que
para el punto P1 será: -j1 y para P2 +j1, es decir la
reactancia del signo opuesto a la que presenta la línea en esos
puntos.
Desnormalizando, el elemento en serie será
para P1, 50 Ohms capacitivos y para P2 50 Ohms inductivos (el valor 50,
que coincide con Zo, es simple coincidencia)
Variante en paralelo
El procedimiento explicado es correcto,
pero adolece de un inconveniente: Ha resuelto el problema de la
adaptación pero supone que la cancelación de la reactancia se efectuará
con un elemento en serie. En la práctica, especialmente con
cables coaxiles y por conveniencias mecánicas, resulta mejor realizar la
cancelación con elementos conectados en derivación (en paralelo). Esto
también es fácil resolver:
En
vez de utilizar el concepto de Impedancia utilizaremos el de Admitancia,
de esa manera nuestra carga de 20 - j10 la convertimos a su equivalente
en Admitancia según lo visto en "Convirtiendo Impedancias en
Admitancias y viceversa".
ZL = 20 - j10
Normalizando
ZN = (20 - j10) / 50 = 0,4 - j0,2 Convirtiendo a Admitancia con el
ábaco obtenemos:
YN = 2 +
j1 que desnormalizado es
YL = (2 + j1) x 0,02 =
0,04 + j0,02 Mho
(Recordando que, si Zo = 50 Ohms
=> Yo = 1 / Zo = 1 / 50 Ohms =
0,02 Mho que será la Admitancia
correspondiente de la línea de 50 Ohms y que emplearemos para normalizar
o desnormalizar nuestras Admitancias, Conductancias y
susceptancias).
Trazamos una semirrecta que partiendo del
centro pase por el punto Y = 2 +
j1 y corte la escala WAVELENGHT TOWARD GENERATOR donde
leemos l = 0,211.
Nuestra meta ahora será encontrar un par de
puntos en el círculo de Gamma constante en que la Conductancia sea
1 (que desnormalizada representa una
Conductancia de 0,02 Mho que, a su vez, equivale a una Resistencia de 50
Ohms).
Vemos en el gráfico que, al igual
antes, encontramos dos puntos (P1 y
P2) con G = 1, P1 tiene
asociada una Susceptancia capacitiva (B = +j1) y P2 una inductiva (B = -J1). Igual que en el
ejemplo anterior, trazando sendas líneas que pasando por esos puntos
alcancen la escala WAVELENGHT TOWARD GENERATOR, leemos sobre ellas dos
valores: l1 = 0,161 y l2 = 0,338
; calcularemos la distancia
para para el P2 dejando la que
corresponda a P1 como ejercicio para
el lector.
Para obtener la distancia en longitudes de onda entre
l2 y l,
simplemente los restamos:
l2 - l = 0,338 -
0,211 = 0,127
entonces, en el punto que se halla a 0,127
l de la
carga podremos conectar en paralelo una Susceptancia inductiva de
-jB1 con lo cual nuevamente hemos
logrado adaptar nuevamente la línea. De esta forma, con una simple "T"
podríamos conectar en un coaxil un trozo de cable que a la frecuencia
produzca ese valor de Inductancia. Tenemos asi conformado un "Stub" a
toda regla. Y lo más interesante de todo, gracias al ábaco de
Smith...
Volver
al índice
Medición de la impedancia de carga
con un voltímetro y un medidor de ROE
La medición de una impedancia en RF
generalmente requiere instrumental que no está al alcance del aficionado
medio, especialmente en FME. Los instrumentos sencillos habitualmente
producen más problemas de los que solucionan y la tarea se torna
insegura, sin embargo con un medidor de ROE, unas secciones de línea, un
elemental medidor de tensión de radiofrecuencia (que hasta puede ser
simplemente una lámpara de Neón), una cinta métrica (y cierta dosis de
paciencia indispensable) pueden efectuarse mediciones muy precisas de
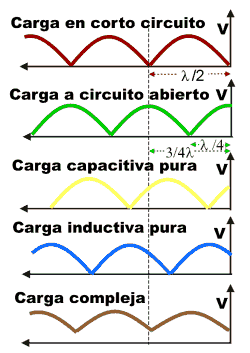
impedancia. Para ello recordemos la distribución de tensión en una línea
para casos extremos.
En
la figura, el lado de la carga es el derecho y el del generador el
izquierdo).
Vemos en la figura que para una carga que sea un
cortocircuito, el primer mínimo de tensión se halla a 1/2
l medido desde
la carga hacia el generador (sin contar el mínimo que se produce justo
sobre la carga).
Para una carga que fuera un circuito
abierto el primer mínimo se encuentra exactamente a 1/4
l medido hacia
el generador, pero si observamos cuidadosamente notaremos que el segundo
mínimo se encuentra a 3/4 l (1/4 + 1/2) hacia el generador, si lo midiéramos
contando a partir del mínimo de cortocircuito, encontraremos que está a
1/4 l de este
hacia el generador. Tengamos en cuenta esto pues luego, en los ejemplos,
emplearemos como punto de referencia un mínimo de
cortocircuito.
(La figura muestra la tensión para carga
capacitiva o inductiva pura de valor normalizado 1).
En el caso de una carga capacitiva el
primer mínimo se encuentra a una distancia menor de 1/4
l medida desde
la carga hacia el generador (y por ende también menor de 1/4
l de cualquier
mínimo de cortocircuito).
En el caso de una carga inductiva el mínimo
se hallará a una distancia algo mayor de 1/4 l pero menor que 1/2
l hacia
generador, medido desde la carga o desde un mínimo de
cortocircuito.
Este comportamiento es muy importante pues
nos permite conocer el carácter de una carga con solo conocer a qué
distancia se halla del primer mínimo de cortocircuito.
Desde luego que es posible trabajar
midiendo distancias directamente desde la carga, pero preferimos emplear
un mínimo de referencia pues servirá para conocer la impedancia de una
antena estando alejados de ella, entonces una vez que obtenemos un
mínimo de cortocircuito cercano a nuestro lugar de trabajo lo
señalaremos y tomaremos las medidas a partir de él; no obstante esto es
correcto hacerlo así solo si las pérdidas de la líneas son bajas
pudiéndosela considerar sin pérdida para los fines prácticos. Se puede
tomar como una base razonable que la atenuación sea menor a 1
dB.
Los gráficos de tensión sobre la línea de
la figura son para casos extremos: cortocircuito, circuito abierto,
reactancias puras, etc. por eso los mínimos de tensión alcanzan 0 V,
pero lo más normal será encontrar impedancias de carga complejas, es
decir que poseen tanto resistencia como reactancia, en estos casos la
posición de los mínimos y los máximos son muy semejantes a los que hemos
visto pero serán simplemente "mínimos" que no necesariamente alcanzarán
0V; entonces:
Si la posición del mínimo no nulo es
la que correspondería a un circuito abierto es porque la
impedancia tiene un valor mayor que Zo y es puramente
resistiva.
Si la posición del mínimo no nulo es
la que correspondería a un cortocircuito es debido a que la
impedancia de carga tiene un valor menor que Zo y es puramente
resistiva.
Del mismo modo se razona para cargas
capacitivas e inductivas.
Analicemos el siguiente ejemplo:
Tenemos una carga desconocida y deseamos
conocer su impedancia para ello:
- Medimos la ROE de la línea y obtenemos
ROE = 3 : 1
- Trazamos el círculo de Gamma constante
que pasa por este valor.
- Cortocircuitamos la línea en el extremo
de la carga y ubicamos un mínimo en la línea que nos resulte cómodo
para trabajar, el cual tomaremos como referencia.
- Conectamos nuevamente la carga y
buscamos con el voltímetro o sonda de RF el primer mínimo de tensión
que se encuentre partiendo desde el punto de referencia en dirección a
la carga. Supongamos que lo encontramos a 0,069 l de longitud de onda
respecto del mínimo de referencia.
- Puesto que está a menos de 1/4
l de
distancia, ya estamos en condiciones de inferir que la carga es de
naturaleza capacitiva.
Entonces:
- Sabemos que la impedancia desconocida
debe hallarse en algún punto del círculo de Gamma constante que hemos
dibujado.
- Sabemos que siendo capacitiva el punto
estará situado en la porción de círculo de Gamma constante inferior,
que es donde se hallan en el ábaco las reactancias capacitivas.
- Sabemos, por lo ya visto, que podemos
trazar en el ábaco una semirrecta cuyo origen sea el valor 1 (el
centro) que pase por el punto que representa a la impedancia hasta
cortar a la escala exterior calibrada en longitudes de onda. Entonces,
si nos desplazamos por la escala exterior desde ese punto hacia el
generador hasta llegar al eje de los reales en el punto 0 obtenemos la
distancia en longitudes de onda desde la carga hasta un mínimo de
tensión.
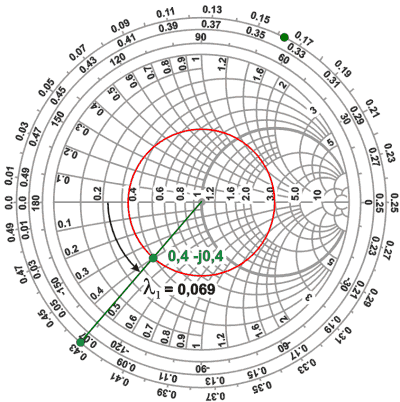Entonces, en nuestro problema, solo será cuestión de hallar
sobre el semicírculo de Gamma constante correspondiente a reactancias
capacitivas un punto tal que cumpla con la condición de que yendo 0,069
l (en coaxil)
hacia el generador alcance justo al eje de los reales en el punto 0
(cortocircuito). Ese punto será entonces el valor de la impedancia que
nos interesa conocer.
Naturalmente, una vez comprendida la idea,
en la práctica procedemos a la inversa, es decir: midiendo sobre la
escala periférica calibrada en longitudes de onda 0,069 l contando desde el punto 0
hacia la carga del lado de las
reactancia capacitiva y desde ese punto trazamos una línea hacia el
centro del ábaco. Donde la línea corta al círculo de Gamma constante
obtendremos el valor de la impedancia normalizado correspondiente a esa
carga.
ZN = 0,4 - j0,4
desnormalizándolo obtenemos
Z = ZN x Zo = (0,4 - j0,4)
x 50 = 20 - j20 W
Este procedimiento que es fácil de
comprender se aplica directamente con líneas abiertas, pero empleando el
ingenio puede emplearse algún trozo de coaxil, construido al efecto, con
"perforaciones" destinadas a tocar el conductor central con el
voltímetro. Para un "instrumento" tan capaz no es una inversión muy
cara... En FME se emplean líneas coaxiles ranuradas, conocidas como
"slotted lines" que permiten un desplazamiento continuo de la punta del
voltímetro.
Bibliografía
consultada:
-
"Ingeniería de radio".
Frederick Emmons Terman.
-
Application Note AN671.
Motorola.
-
"How to use the Smith
Chart". James R. fisk, W1HR, Ham Radio Magazine, Marzo 1978